Программирование трехмерной графики. Часть 2.

2.1. Перемещение - операция Translate.

2.2. Поворот вокруг координатной оси – операция Rotate.

2.3. Масштабирование – операция Scale.

2.4. Итог.

В предыдущей статье мы познакомились с основами программирования трехмерной графики. Научились строить трехмерные точки и проецировать их на экран нашего монитора. Итак, мы уже можем отобразить точку на мониторе. Теперь пора научится основным операциям по манипуляции этой точки в трехмерном пространстве. А именно:

2.1. Перемещение - операция Translate.

Как уже понятно из ее названия, перемещает точку в заданном направлении, на заданной расстояние. Допустим, у нас есть точка:

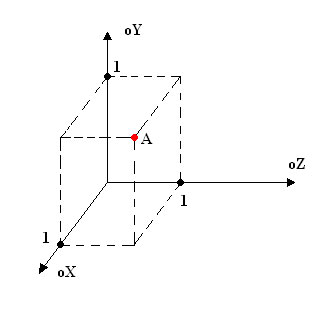
Что бы переместить ее, например, по оси Z на единицу, нужно проделать вот такою простую операцию:

У нас получится новая точка с координатами:

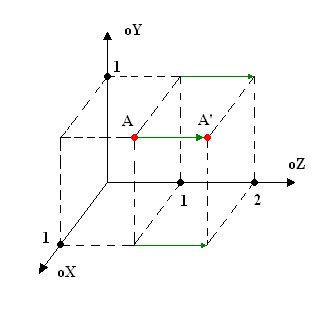
Процедуру перемещение точки\вершины на паскале, можно описать следующим образом:

2.2. Поворот вокруг координатной оси – операция Rotate.

Самая сложная по вычислениям операция. А так же самая затратная в плане производительности (на ее тратится в несколько раз больше компьютерных ресурсов, чем на другие операции).

Что бы разобраться как осуществляется поворот геометрических объектов, нужно сначала понять, что такое синус и косинус, а так же разобраться в формуле окружности.

Итак, что бы осуществлять поворот точек, прежде всего нам понадобится две тригонометрические функции:

• Синус (sin x)
• Косинус (cos x)

Прежде всего, нам нужно знать, что синус и косинус – это периодические функции, и областью значений этих функций является отрезок [–1; 1]. Т.е. какие-либо значение мы не подставляли бы в данные функции вместо x, например sin 0.1; cos 123, sin 1/2, cos 1.2; - значение функции, всегда будет лежать в интервале от – 1 до 1. Можете это сами проверить на калькуляторе, вычисляя значение этих функций для разных чисел.

Следующим свойством данных функций является их периодичность. Это означает что по мере увеличения аргумента x, эти функция все время будут колебаться в интервале от нуля до единицы. Посмотрите на графики этих функций, рисунок 2.2.1.

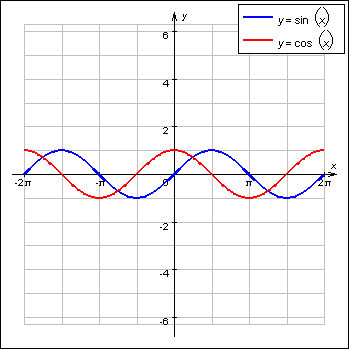
На этих графиках видно, что данные функции совершают полное колебательное движение, в интервале значений x: [0; 2pi]. Т.е. при прохождении функций через данный интервал, они опять приходят в исходное положение, которое было при значении x = 0. Потом совершается новое, точно такое же колебательное движение, но уже при x: [2pi; 4pi], и так до бесконечности. Это свойство и называется периодичностью функций.

Что такое число пи (pi) мы сейчас разбирать не будем, нам нужно только знать, что это математическая константа, число с бесконечной дробью, округленное значение которого равно = 3,14.

Это число имеется во всех языках программирования, поэтому самому его задавать не нужно. Просто иногда, что бы начать пользоваться этим числом, в некоторых средах нужно сначала подключить соответствующую математическую библиотеку.

С понятиями синуса и косинуса, тесно связанно понятие окружности. Дело в том, что, по сути, окружность – это тоже колебательная система. Что бы было проще, давайте сначала рассмотри все эти формулы в двухмерной плоскости.

Допустим, что в двухмерной системе координат у нас заданна точка с координатами A(1, 1); Рисунок 2.2.2.

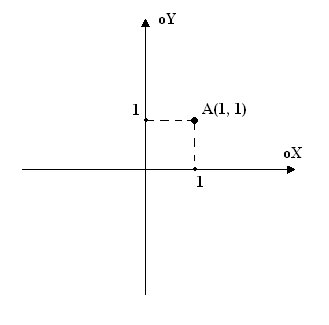
Так вот, эту точку мы можем вращать вокруг начала координат с помощью этих формул:

X, Y – координаты точки. Alpha – угол на который мы хотим повернуть точку, может изменяться от 0 до 2pi.X1, Y1 - новые координаты точки, полученные в результате поворота.

Так же с помощью этих формул, можно легко нарисовать окружность. Достаточно подставлять в данную формулу вместо Alpha значения от 0 до 2pi. У нас получится вот такая картинка: (Рисунок 2.2.3).

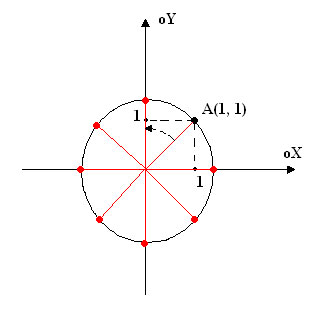
На этом рисунке мы поворачиваем исходную точку A(1, 1) (она у нас черного цвета), каждый раз на 45 градусов, или на значение Alpha = pi / 4. (красные точки). В итоге мы видим, что при полном повороте мы опять пришли в нашу исходную точку A. Также мы видим, что значение Alpha стало равно = 2*Pi или 360 градусов.

Ну вот, мы научились вертеть точки вокруг своей оси в двухмерной плоскости. Как же теперь проделать эту операцию в трехмерной системе координат? Да точно так же! Формулы абсолютно те же! Просто в двухмерной системе координат у нас всего одна плоскость – XY. А в трехмерной, таких плоскостей три: XY, YZ и XZ. Что бы крутить их в данных плоскостях, нужно использовать соответствующие формулы:

Что бы одновременно крутить точки по осям, данные формулы нужно использовать поочередно.

Процедуры поворота точек\вершин на паскале, можно описать следующим образом:

2.3. Масштабирование.

Пожалуй, самая простая операция. Что выполнить масштабирование, нужно каждую координату точки умножить на соответствующий коэффициент.

где k - коэффициент масштабирования. Если k > 1 – то размеры масштабируемого объекта увеличиваются, (мы приближаемся к объекту), если K < 1, то соответственно размеры объекта уменьшаются, (отдаляемся от объекта).

Процедуры масштабирования точек\вершин на паскале, можно описать следующим образом:

2.4. Итог.

Итак, мы научились выполнять основные операции по манипуляции точками в пространстве. Осталось только на практике посмотреть, как все это работает. Ниже вы можете скачать исходник Delphi демонстрирующий работу этих трех операций.

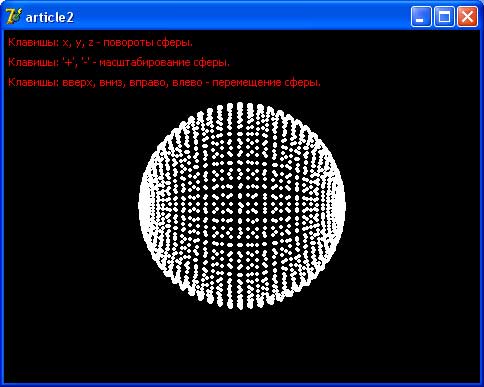
В данном примере генерируется трехмерная сфера, которую можно перемещать, вращать и масштабировать.

• Клавишы: x, y, z - повороты сферы.
• Клавишы: '+', '-' - масштабирование сферы.
• Клавишы: вверх, вниз, вправо, влево - перемещение сферы.

Скачать исходник Delphi. [4 Кб]